

y2 = 4px
Los planetas del Sistema Solar se mueven alrededor del Sol recorriendo
trayectorias, también llamadas órbitas, elípticas. Todos los planetas
viajan en el mismo sentido pero se mueven a distintas velocidades, de
manera que barren áreas iguales en tiempos iguales; por este motivo
los planetas más alejados del Sol se mueven más lentamente.
Las trayectorias de los cuerpos celestes son curvas que pertenecen a la
familia de las cónicas, es decir, elipses, parábolas e hipérbolas. Las ecuaciones
de estas curvas en coordenadas cartesianas son:


y2 = 4px

Las órbitas elípticas tiene al Sol en el foco; el punto de la elipse más cercano al Sol se llama el perihelio y el más alejado el afelio. La mayor parte de los cuerpos del Sistema Solar (planetas, cometas, asteroides...) siguen trayectorias elípticas aunque con excentricidades muy diferentes.
Si la distancia del planeta al Sol en el perihelio es parecida a la distancia en el afelio, la elipse tiene una excentricidad pequeña: la órbita es casi circular. Los planetas pertenecen a este grupo.
Por el contrario si la distancia del planeta al Sol en el perihelio es mucho menor que en el afelio, la elipse tiene una excentricidad muy pequeña: la órbita es casi una parábola. Los cometas, y algunos cuerpos menores del Sistema Solar tienen órbitas de este tipo.
Los cuerpos con trayectoria hiperbólica no están atrapados por la gravedad del Sol y pueden escapar del Sistema Solar. Puesto que el Sistema Solar es bastante viejo, el número de cuerpos con trayectoria hiperbólica es muy pequeño: algunos fragmentos de roca desprendidos en las colisiones entre cuerpos del Sistema Solar (por ejemplo en la corrientes de meteoroides o en el cinturón de asteroides) y las sondas espaciales diseñadas para este propósito (por ejemplo los Pioneer o los Voyager de la NASA).
En la siguiente tabla se resumen las expresiones algunos datos de interés de las cónicas:
| Círculo | Elipse | Parábola | Hipérbola | |
|---|---|---|---|---|
| Ecuación | x2 + y2 = r2 |  |
y2 = 4px |  |
| Parámetros | r = el radio del círculo |
a = el radio mayor (= 1/2 de la longitud del eje mayor) b = el radio menor (= 1/2 de la longitud del eje menor) c = la distancia desde el centro al foco |
p = la distancia desde el vértice al foco (o a la directriz) |
a = 1/2 de la longitud del eje mayor b = 1/2 de la longitud del eje menor c = la distancia desde el centro al foco |
| Excentricidad (c/a) | 0 | (0,1) | 1 | >1 |
| Relación al foco | p = 0 | a2 - b2 = c2 | p = p | a2 + b2 = c2 |
| Definición geométrica | Lugar geométrico de los puntos que equidistan del origen | Lugar geométrico de los puntos cuya suma de distancias a cada foco es constante | Lugar geométrico de los puntos cuya distancia al foco es igual a la distancia a la directriz | Lugar geométrico de los puntos cuya diferencia entre las distancias a cada foco es constante |
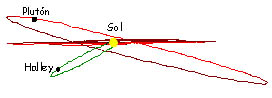
Aunque las órbitas de todos los planetas son elipses, no todas las elipses estan alineadas ni todas las elipses están en el mismo plano. En general, la mayor parte de las planetas orbitan en planos muy cercanos al plano de la órbita la terrestre, también denominado eclíptica. La excepción es Plutón, cuyo plano orbital está inclinado más de 17º con respecto a la eclíptica
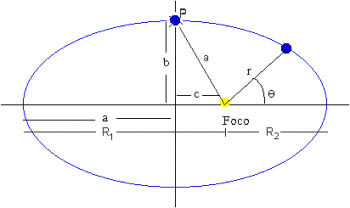
Para resolver los ejercicios de órbitas vas a tener que saber formular en ecuaciones cartesianas la ecuación de una elipse cuyos ejes de simetría está rotados con respecto a tus ejes cartesianos. Si te fijas en el dibujo y las expresiones que están más abajo, verás que no es tan difícil... Vamos a desarrollar algunas propiedades de los puntos y elementos de una elipse fijándonos en la figura.
La relación entre un punto P de la elipse y el foco de la misma es:
a2 = b2 + c2
Existe una relación entre las dos distancias al foco, R1 y R2, y es la siguiente:
R1 - R2 = 2c
R1 = a + c
Las siguientes relaciones servirán para determinar los distintos elementos de la elipse:
R1 = a(1-e)
R2 = a(1+e)
R1 + R2 = 2a
b2 = a2(1-e2)
De manera que la ecuación cartesiana de la elipse será:

Si la elipse está girada un ángulo "ω" con respecto al eje X, la formulación se complica un poco:
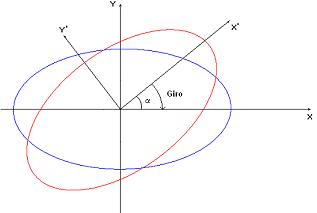
entonces la fórmula de la elipse en el sistema X'Y' sería la habitual:

pero para escribirla en el sistema XY habría que aplicar la siguiente transformación:
x' = x·cosα - y·senα
y' = x·senα + y·cosα
con lo que obtenemos:

y de aquí se obtiene la expresión (y los coeficientes) que teneis que rellenar y calcular en el ejercicio:
x2(b2cos2α + a2sen2α) + y2(b2sen2α + a2cos2α) + 2xysenαcosα(a2 - b2) - a2b2 = 0
Se sabe, por otro lado, que la ecuación general de una cónica es la siguiente:
Ax2 + By2 + Cxy + D = 0
y comparando las dos ecuaciones ves claramente que:
b2cos2α + a2sen2α = A
b2sen2α + a2cos2α = B
2senαcosα(a2 - b2) = C
-a2b2 = D