Command disabled: backlink
Probabilidad Total
Tenemos n sucesos 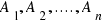 que son:
que son:
- incompatibles dos a dos, es decir, no tienen ningún elemento en común (
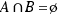 )
)
- si uno todos los sucesos da E (espacio muestral), conjunto de todos los posibles resultados de una experiencia aleatoria.
Es decir: 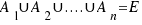
Entonces, la probabilidad de que ocurra un suceso S lo puedo descomponer como:
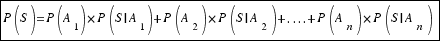 (Demostración de este resultado)
(Demostración de este resultado)
Ejemplo
Un ratón es perseguido por un hambriento gato. El ratón puede entrar por uno de los callejones A, B ó C, para intentar salvarse.
- La probabilidad de que el ratón entre en el callejón A es de 0.3
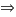 P(A)=0.3
P(A)=0.3 - La probabilidad de que el ratón entre en el callejón B es de 0.5
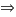 P(B)=0.5
P(B)=0.5 - La probabilidad de que el ratón entre en el callejón C es de 0.2
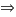 P(C)=0.2
P(C)=0.2
Las probabilidades de que el gato cace al ratoncillo en cada callejón son:
- P(gato cace al ratón en A)= P(+|A)= 0.4
- P(gato cace al ratón en B)= P(+|B)= 0.6
- P(gato cace al ratón en C)= P(+|C)= 0.1

Calcular la probabilidad de que el gato cace al ratón.(Calcular P(+))
SOLUCIÓN
Construimos el diagrama de árbol asociado al ejercicio:
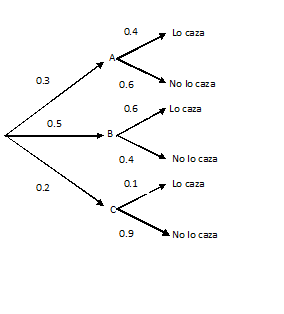
P(+)=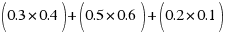 =
=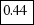 ¡El gato no tiene la merienda muy asegurada!
¡El gato no tiene la merienda muy asegurada!




