ECUACIONES DE SEGUNDO GRADO BÁSICAS
Ejemplo
Primero vamos a ver una demostración visual de una ecuación de segundo grado con un ejemplo:
Resolvamos la ecuación 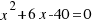 .
.
Solución
Pasamos el término independiente al otro miembro: 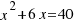 .
.
El primer sumando 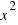 , se corresponde con el área del cuadrado de lado
, se corresponde con el área del cuadrado de lado 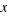 , y el segundo sumando
, y el segundo sumando 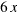 , se corresponde con el área del rectángulo de lados
, se corresponde con el área del rectángulo de lados 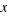 y
y 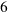 , como se indica en el siguiente dibujo:
, como se indica en el siguiente dibujo:

El rectángulo lo descomponemos en dos rectángulos iguales de lados 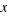 y
y 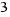 y pasamos uno de ellos justo debajo del cuadrado de lado
y pasamos uno de ellos justo debajo del cuadrado de lado 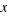 .
.

Y ahora se añade el cuadrado de área 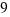 , del espacio que queda en la esquina inferior derecha, y así obtenemos un cuadrado perfecto de lado
, del espacio que queda en la esquina inferior derecha, y así obtenemos un cuadrado perfecto de lado 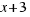 .
.
Como hemos añadido un cuadrado de área 9, hemos modificado nuestra ecuación inicial, y por tanto, ahora tenemos que sumar 9 a ambos miembros de la ecuación, obteniendo: 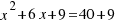 , así el miembro de la izquierda de la ecuación es el cuadrado perfecto:
, así el miembro de la izquierda de la ecuación es el cuadrado perfecto: 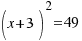 .
.
Haciendo la raíz cuadrada en los dos miembros nos queda:
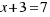
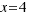
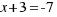
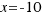
La solución 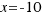 no tiene sentido en geometría, pero sí es solución de la ecuación dada.
no tiene sentido en geometría, pero sí es solución de la ecuación dada.
Ejercicio.
Intenta resolver la ecuación 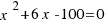 , de la misma manera que lo hemos hecho en el ejemplo anterior. Como ayuda te damos la siguiente aplicación con la que puedes practicar las figuras que van quedando al resolver la ecuación. Para ello, toma el punto
, de la misma manera que lo hemos hecho en el ejemplo anterior. Como ayuda te damos la siguiente aplicación con la que puedes practicar las figuras que van quedando al resolver la ecuación. Para ello, toma el punto  del segmento que hay arriba a la izquierda de la aplicación y muévelo según creas conveniente.
del segmento que hay arriba a la izquierda de la aplicación y muévelo según creas conveniente.
Si no se puede ver la siguiente aplicación, se puede descargar JAVA en la dirección: http://www.houspain.com/gttp/salsaj
Caso general
Ahora hacemos los mismos pasos para una ecuación de segundo grado en general: 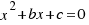 , y llegaríamos a la solución
, y llegaríamos a la solución 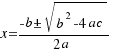 . El radicando
. El radicando 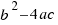 recibe el nombre de discriminante.
recibe el nombre de discriminante.

Tenemos la ecuación 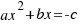 , multiplicamos los dos miembros de la ecuación por
, multiplicamos los dos miembros de la ecuación por 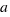 para que nos quede un cuadrado perfecto de lado
para que nos quede un cuadrado perfecto de lado 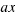 , y así nos será más sencillo operar, entonces nos queda la ecuación
, y así nos será más sencillo operar, entonces nos queda la ecuación 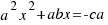 .
.
El primer sumando 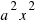 , es el área del cuadrado de lado
, es el área del cuadrado de lado 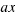 y el segundo sumando
y el segundo sumando 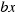 , es el área de un rectángulo de lados
, es el área de un rectángulo de lados 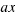 y
y 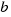 .
.
Descomponemos el rectángulo en otros dos rectángulos de lados 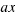 y
y 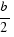 , como se observa en la figura siguiente:
, como se observa en la figura siguiente:

Añadiendo el cuadrado de área 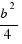 que falta en la figura (esquina inferior derecha), tendremos un cuadrado perfecto de lado
que falta en la figura (esquina inferior derecha), tendremos un cuadrado perfecto de lado 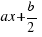 , entonces sumamos
, entonces sumamos 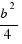 a los dos miembros de la ecuación, quedándonos:
a los dos miembros de la ecuación, quedándonos: 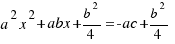 , multiplicamos los dos miembros por 4 para que nos quede más sencillo:
, multiplicamos los dos miembros por 4 para que nos quede más sencillo: 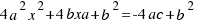 .
.
El miembro de la izquierda de esta última ecuación es el siguiente cuadrado perfecto: 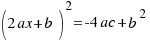 .
.
Haciendo la raíz cuadrada en los dos miembros queda:
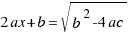
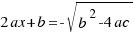
Por tanto, las soluciones a nuestra ecuación 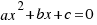 son (despejando
son (despejando 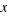 de las dos últimas ecuaciones):
de las dos últimas ecuaciones):
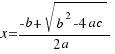
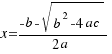
Al radicando 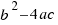 lo llamaremos discriminante y lo representaremos con la letra
lo llamaremos discriminante y lo representaremos con la letra 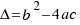 . Podemos tener varios casos en las soluciones de nuestra ecuación según sea el discriminante:
. Podemos tener varios casos en las soluciones de nuestra ecuación según sea el discriminante:
1.- Si ∆ > 0, la ecuación 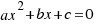 tiene dos soluciones reales y distintas:
tiene dos soluciones reales y distintas:
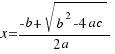
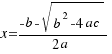
2.- Si ∆ = 0, la ecuación 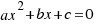 tiene una solución doble:
tiene una solución doble:
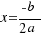
3.- Si ∆ < 0, la ecuación 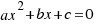 no tiene soluciones reales.
no tiene soluciones reales.
LOS NÚMEROS COMPLEJOS
Hasta ahora cuando en las ecuaciones de segundo grado teníamos que ∆ < 0, decíamos que no es posible hallar la raíz cuadrada de un número negativo, y por tanto, la ecuación no tenía solución. Pero en algún momento, los matemáticos decidieron poner solución a este problema tratando a 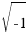 como un número real. El matemático Leibnitz decía que
como un número real. El matemático Leibnitz decía que 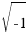 era una especie de anfibio entre el ser y la nada.
era una especie de anfibio entre el ser y la nada.
Euler, en el año 1777 denominó a 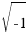 como número imaginario
como número imaginario 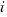 . Este número imaginario operado elementalmente con los reales, dio lugar a los números complejos.
. Este número imaginario operado elementalmente con los reales, dio lugar a los números complejos. 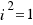 .
.
Los números complejos son las expresiones del tipo 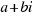 , donde a y b son números reales. El término que no acompaña a la
, donde a y b son números reales. El término que no acompaña a la 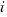 (
(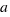 ), recibe el nombre de parte real, y el término que acompaña a
), recibe el nombre de parte real, y el término que acompaña a 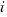 (
(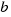 ), recibe el nombre de parte imaginaria. Cuando la parte imaginaria es cero, lo que tenemos es un número real. Los números complejos se pueden representar en el plano de la siguiente manera:
), recibe el nombre de parte imaginaria. Cuando la parte imaginaria es cero, lo que tenemos es un número real. Los números complejos se pueden representar en el plano de la siguiente manera:
La parte real se representa en el eje X (también denominado eje real).
La parte imaginaria se representa en el eje Y (también denominado eje imaginario).
Ejemplo:

OPERACIONES CON NÚMEROS COMPLEJOS
Suma: 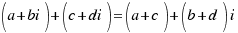
Resta: 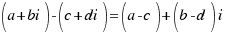
Multiplicación: 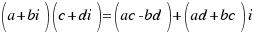
NOTA: El producto de un número complejo por su conjugado es siempre un número real:
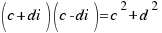
División: 
NOTA: No se puede dividir por cero.
FORMA POLAR DE LOS NÚMEROS COMPLEJOS
A la representación de los números complejos: 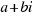 se le denomina coordenadas ortogonales, y en algunas ocasiones es más conveniente utilizar otra representación, la forma polar.
se le denomina coordenadas ortogonales, y en algunas ocasiones es más conveniente utilizar otra representación, la forma polar.
Representemos el número complejo 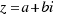 , en el plano de los números complejos como un punto con coordenadas (a,b). Llamaremos r (módulo del número complejo z) a la distancia desde el punto (0,0) hasta el punto (a,b). Y denominaremos
, en el plano de los números complejos como un punto con coordenadas (a,b). Llamaremos r (módulo del número complejo z) a la distancia desde el punto (0,0) hasta el punto (a,b). Y denominaremos 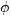 (argumento del número complejo) al ángulo que forma la distancia r con respecto al eje positivo, el eje X, como se muestra en la figura siguiente:
(argumento del número complejo) al ángulo que forma la distancia r con respecto al eje positivo, el eje X, como se muestra en la figura siguiente:

La representación polar de un número complejo z, nos permite representarlo en función de r y 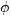 , (r,
, (r, 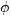 ). Así, tenemos:
). Así, tenemos:
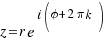 , con k = 1,2, ……
, con k = 1,2, ……