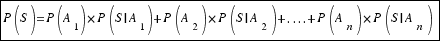Demostración resultado Probabilidad Total
FALTA DOS DIBUJOS DIAGRAMAS
Descomponemos S en sucesos incompatibles: 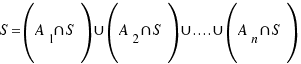
Aplicando a esto la propiedad que dice: ”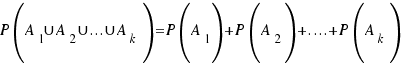 siendo
siendo 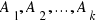 sucesos incompatibles dos a dos” resulta:
sucesos incompatibles dos a dos” resulta:
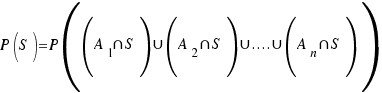 =
=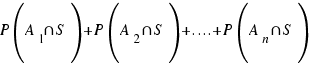
Teniendo en cuenta el significado de la probabilidad condicionada, que mide la proporción de veces que ocurre A de entre las que ocurre C:
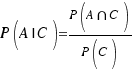
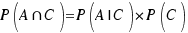
Obtenemos lo que queríamos demostrar: