Equations of second degree.
Example.
We will do a geometric proof with an example.
What is the solution to the following equation: 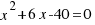 ?
?
Solution.
We move the independent term to the other side: 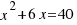 .
.
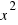 is the area of a square with side
is the area of a square with side 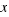 .
. 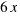 is the area of a rectangle with sides
is the area of a rectangle with sides 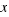 and
and 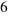 . We can see this square and rectangle in the following figure:
. We can see this square and rectangle in the following figure:

With the rectangle of the figure, we construct two rectangles equals, with sides 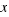 and
and  , and we move one of these rectangles under of the square of the figure:
, and we move one of these rectangles under of the square of the figure:

Now, we also have a square with area 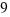 , down in the fiugure, in the right corner. Finally, we obtain with all these figures, one square with side
, down in the fiugure, in the right corner. Finally, we obtain with all these figures, one square with side 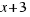 .
.
When we have added the square with area 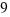 , we have changed our initial equation, and we have that add
, we have changed our initial equation, and we have that add 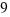 to both sides of the equation:
to both sides of the equation: 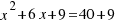 . Now,
. Now, 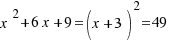 and
and 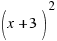 is a square with side
is a square with side 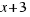 .
.
In both sides of equation we do the square root:
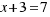
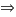
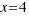
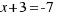
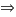
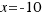
The solution 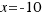 is impossible in geometric, because it is negative, but it is solution of our equation.
is impossible in geometric, because it is negative, but it is solution of our equation.
Exercise.
You try to solve the following equation: 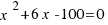 as in the previous example. You can to solve the equation by using the following application. To you use the application, you can to move the point
as in the previous example. You can to solve the equation by using the following application. To you use the application, you can to move the point 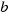 , this point is in the segment that it is up on the left in the application. you must move the point to the figure to be right.
, this point is in the segment that it is up on the left in the application. you must move the point to the figure to be right.
If you can not to see the application you can to download JAVA in the next web site: http://www.houspain.com/gttp/salsaj
General case.
We are doing the same steps of the previous example, but now we are doing for any equation of second degree: 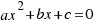 , and we will obtain the solution:
, and we will obtain the solution: 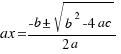 .
.
We have the following figure to solve the equation: 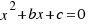 :
:

We want to get a square with side 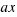 , for this we multiply both sides of our equation per
, for this we multiply both sides of our equation per 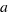 . Now the calculations are easier and we have the equation:
. Now the calculations are easier and we have the equation: 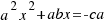 .
.
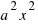 is the area of the square with side
is the area of the square with side 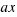 , and
, and 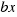 is the area of the rectangle with sides
is the area of the rectangle with sides 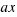 and
and 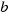 . With this rectangle, we construct two rectangles with sides
. With this rectangle, we construct two rectangles with sides 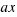 and
and 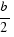 as in the following figure:
as in the following figure:

We add the square with area 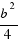 (it is down in the figure, in the right corner). Now we have a square with side
(it is down in the figure, in the right corner). Now we have a square with side 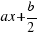 . When we have added this square to the figure, we have changed our initial equation, and we have that add
. When we have added this square to the figure, we have changed our initial equation, and we have that add 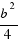 to both sides of the equation:
to both sides of the equation: 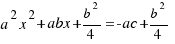 . We multiply both sides of the last equation per 4:
. We multiply both sides of the last equation per 4: 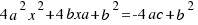 , and now the calculations are easier.
, and now the calculations are easier.
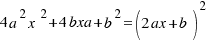 is the area of a square with side
is the area of a square with side 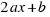 . Our equation is:
. Our equation is: 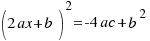 .
.
We do the square root in both sides of the last equation, and we obtain:
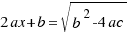
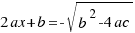
We work out the value of 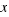 in the last two equations, and the solutions of our equation are:
in the last two equations, and the solutions of our equation are:
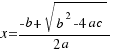
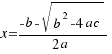
We will represent to 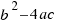 with the letter:
with the letter: 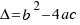 . We can to have several solutions depending of the different values of
. We can to have several solutions depending of the different values of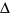 :
:
1.- If ∆ > 0, the equation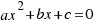 have two real solutionts differents:
have two real solutionts differents:
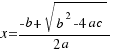
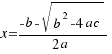
2.- If ∆ = 0, the equation 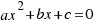 have a double solution:
have a double solution:
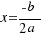
3.- If ∆ < 0, the equation 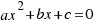 have not real solutions.
have not real solutions.