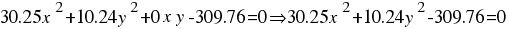Ejemplo numérico de cómo calcular la ecuación de una elipse.

Supongamos que a=5.5, 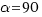alpha=90 , b=3.2.

Calculamos los valores A, B, C y D con las siguientes fórmulas:

$A = b^2 {cos^2 (alpha)} + a^2 {sen^2 (alpha)} = (3.2)^2 {cos^2 90º} + (5.5)^2 {sen^2 90º} = 30.25$

$B = b^2 {sen^2 (alpha)} + a^2 {cos^2 (alpha)} = (3.2)^2 {sen^2 90º} + (5.5)^2 {cos^2 90º} = 10.24$

$C = 2 {sen (alpha)} {cos (alpha)} (a^2 + b^2) = 2 {sen 90º} {cos 90º} ((5.5)^2 - (3.2)^2)$

$D = -(a)^2 {b^2} = - (5.5)^2 {(3.2)^2} = -309.76$

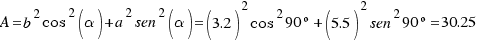
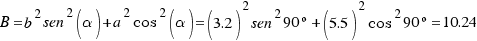
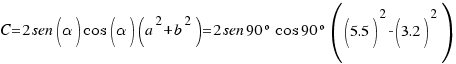
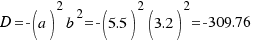
Como la ecuación de una elipse viene dada por:

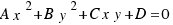A x^2 + B y^2 + C x y + D = 0 , y nosotros ya tenemos calculado los valores A, B C y D, sólo nos queda reemplazar en la última fórmula y tenemos la ecuación de nuestra elipse:

30.25 x^2 + 10.24 y^2 + 0 x y - 309.76 = 0 doubleright 30.25x^2 + 10.24y^2 - 309.76 = 0