Poner en órbita el velero.
- Cálculo de semiejes.
- Cálculo de la ecuación de una elipse.

Poner en órbita el velero.

El objetivo de este ejercicio es el cálculo de la ecuación de una elipse. Para nuestro viaje con el velero estelar es indispensable conocer bien cómo se va a mover por el espacio. Sabemos que se va a mover en una órbita elíptica, de ahí la importancia de calcular la ecuación de una elipse.

FALTA VÍDEO.

Cálculo de semiejes.

En este ejercicio debemos hallar los valores de los semiejes mayor (a) y menor (b). Se pueden hallar eligiendo nosotros qué datos utilizar, teniendo tres casos diferentes:

NOTA: En todos los casos hay que tener en cuenta el radio de la Tierra. Hazte un dibujo de la elipse y en el foco dibuja la Tierra para verlo mejor.

1.- Tenemos la altura sobre la Tierra del perigeo y la altura sobre la Tierra del apogeo.

2.- Tenemos la altura sobre la Tierra del perigeo y la excentricidad.

3.- Tenemos la altura sobre la Tierra del apogeo y la excentricidad.

Dependiendo del caso en el que nos encontremos utilizaremos unas fórmulas u otras. Estas fórmulas son las siguientes:

(1) R_1= a(1-e)

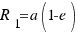
(2) R_2=a(1+e)

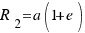
(3) R_1+R_2=2a

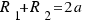
(4) b^2=a^2(1-e^2)

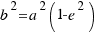
Ahora tienes que darte cuenta de cuál utilizar y cuál no! 8-O

CASO GENERAL

Cálculo de la ecuación de una elipse.

Sabemos que la ecuación de una elipse viene definida por:

Ax^2+By^2+Cxy+D=0

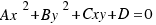
Pero si giramos un ángulo alpha con respecto al eje X, entonces la ecuación de la elipse se complica un poco y obtenemos que:

A = b^2cos^2(alpha)+a^2sin^2(alpha)

B = b^2sin^2(alpha)+a^2cos^2(alpha)

C=2sin(alpha)cos(alpha)(a^2-b^2)

$D = -(a)^2 {b}^2$

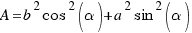
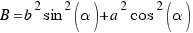
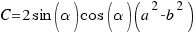
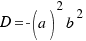
Así pues, para resolver nuestro ejercicio sólo nos hará falta hallar los valores A, B, C y D.

EJEMPLO