PROBABILIDAD A "POSTERIORI". FÓRMULA DE BAYES

En una experiencia compuesta de varios sucesos, como en la siguiente, hay varias formas para llegar a S:

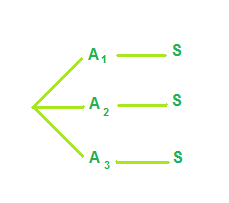
Podemos preguntarnos:¿en qué proporción de dichas formas se pasa por 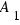{A_1}?

Este tipo de preguntas son resueltas con la Fórmula de Bayes, que dice lo siguiente:


tabular{11}{11}{{P(A_i|S)= {P(A_i)*P(S|A_i)}/{P(A_1)*P(S|A_1)+P(A_2)*P(S|A_2)+....+P(A_n)*P(S|A_n)}}}


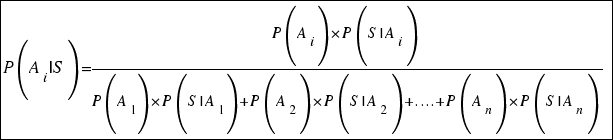
O lo que es equivalente, conociendo el teorema de la probabilidad total:


tabular{11}{11}{{P(A_i|S)= {P(A_i{inter}S)}/{P(S)}}}



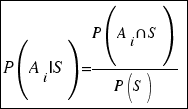
Ejemplo


Un ratón es perseguido por un hambriento gato. El ratón puede entrar por uno de los callejones A,B ó C, para intentar salvarse.

*La probabilidad de que el ratón entre en el callejón A es de 0.3doublerightP(A)=0.3
*La probabilidad de que el ratón entre en el callejón B es de 0.5doublerightP(B)=0.5
*La probabilidad de que el ratón entre en el callejón C es de 0.2doublerightP(C)=0.2

Las probabilidades de que el gato cace al ratoncillo en cada callejón son:

*P(gato cace al ratón en A)= P(+|A)= 0.4
*P(gato cace al ratón en B)= P(+|B)= 0.6
*P(gato cace al ratón en C)= P(+|C)= 0.1



Pasado un tiempo vemos llegar al gato con el ratoncillo en la boca. ¿En cuál de los tres callejones es más probable que el gato haya cazado al ratón?




SOLUCIÓN

Construimos el diagrama de árbol asociado al ejercicio:


Debemos calcular por separado la probabilidad de que el gato haya cazado al ratón en el callejón A, la probabilidad de que el gato haya cazado al ratón en el callejón B y la probabilidad de que lo haya hecho en el callejón C y después comparar esas probabilidades.

La probabilidad de que el gato haya cazado al ratón en el callejón A es:

{P(A|+)= {P(A{inter}+)}/{P(+)}=0.3*0.4/{(0.3*0.4)+(0.5*0.6)+(0.2*0.1)}= 0.12/0.44 = tabular{11}{11}{0.273}}

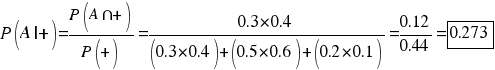
La probabilidad de que el gato haya cazado al ratón en el callejón B es:

{P(B|+)= {P(B{inter}+)}/{P(+)}=0.5*0.6/{(0.3*0.4)+(0.5*0.6)+(0.2*0.1)}= 0.30/0.44 = tabular{11}{11}{0.682}}

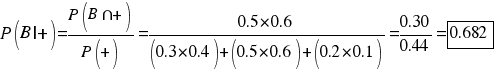
La probabilidad de que el gato haya cazado al ratón en el callejón C es:

{P(C|+)= {P(C{inter}+)}/{P(+)}=0.2*0.1/{(0.3*0.4)+(0.5*0.6)+(0.2*0.1)}= 0.02/0.44 = tabular{11}{11}{0.045}}



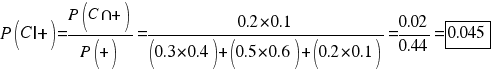
Observamos que es más probable que el gato haya cazado al ratón en el callejón B, ya que aquí la probabilidad es mayor.