Radianes y 0.0174
Definición
Los ángulos se pueden medir en grados o en radianes.
Definimos 1 radián como el valor de un ángulo plano en el que la longitud del arco es igual al radio.
Intuitivamente
¿Qué es un radián?
Si no se pueden ver las aplicaciones de esta página, se puede descargar JAVA en la página
Vamos a ver esta definición en la siguiente aplicación:
- Haz que el arco y el radio midan lo mismo. Para hacer esto mueve el punto amarillo y el radio.
- ¿Cuál es el valor del ángulo
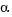 en grados (sexagesimales)?
en grados (sexagesimales)? - Fíjate en el resultado de la división que aparece en la pantalla (longitud del arco entre el radio).
Es 1. Ese ángulo es 1 radian.
- ¿Se puede conseguir con otra medida del radio? ¿Se obtiene el mismo ángulo?
- Pon
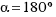 , ¿cuántos radianes crees que son?
, ¿cuántos radianes crees que son?
Fíjate en el resultado de la división que aparece en la pantalla ¿Te suena ese número?
- ¿Y si
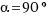 ,
, 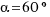 ,
, 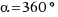 ?
? - ¿Te atreves a dar una relación entre los grados y los radianes?
Formalmente
¿Cuántos grados es 1 radián?
Ya hemos visto gráficamente cómo se halla el valor de 1 radián, ahora vamos a verlo analíticamente (numéricamente).
Nos dicen que 1 radián es el valor de un ángulo plano en el que la longitud del arco es igual al radio.
Un arco de circunferencia es la porción de circunferencia que queda entre dos radios.
La longitud de un arco de circunferencia es 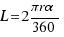 ,
,
donde r es el radio del arco de circunferencia y
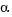 es el ángulo de dicho arco de circunferencia dado en grados.
es el ángulo de dicho arco de circunferencia dado en grados.
Si queremos saber cuántos grados es un radian, según la definición, tenemos que igualar el radio r
con la longitud del arco L, esto es, como 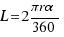 ,
,
al igualarlo a r nos queda 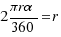 .
.
Por tanto, despejando 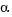 se tiene
se tiene 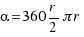 , y simplificando,
, y simplificando,
finalmente llegamos a 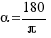 que es el valor de 1 radián en grados.
que es el valor de 1 radián en grados.
¿Cuál es la relación entre grados y radianes?
Un ángulo que abarca una vuelta completa de circunferencia mide 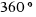 o lo que es lo mismo,
o lo que es lo mismo, 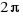 radianes.
radianes.
Así, 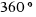 equivalen a
equivalen a 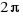 radianes.
radianes.
Y esto nos sirve para pasar de grados a radianes y de radianes a grados,
con una simple regla de tres despejando la x:
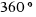 ———
——— 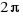 radianes
radianes
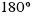 ———- x radianes
———- x radianes
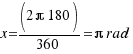 (así,
(así, 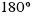 son
son 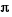 radianes)
radianes)
Utilizando una regla de tres similar (y despejando la x):
- Averigua cómo pasar de grados a radianes calculando cuántos grados es 1 rad.
- Averigua cómo pasar de radianes a grados calculando cuántos radianes es 1°.
En la práctica
De grados a radianes y de radianes a grados
Pasamos de grados a radianes y de radianes a grados:
- ¿Cuántos radianes son
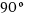 ,
, 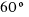 ,
, 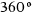 ,
, 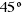 ?
? - ¿Cuántos grados son
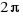 rad,
rad, 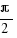 rad,
rad, 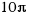 rad,
rad, 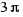 rad?
rad?
Cuando termines puedes comprobar tus soluciones aquí.
Ejercicios relacionados
En cada ejercicio se indican otros conocimientos necesarios.