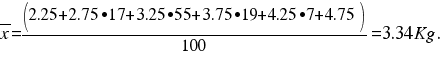Statistic
What is Statistic?
- Statistics: Statistics can be described as the science of classifying and organizing data in order to draw inferences. The collection and organization of data is usually called descriptive statistics; the process of deciding what conclusions may be reached is called inferential statistics.
Example 1: What did we see on television last night?
 We take 8 friends of the our school, and we ask them for the program of television they saw last night. We are doing a statistical study with these datas:
We take 8 friends of the our school, and we ask them for the program of television they saw last night. We are doing a statistical study with these datas:

With these datas, we obtain the following pie chart. This pie chart shows what we friends saw the last night on television:

POPULATION AND SAMPLE
The term data refers to the set of values, elements or numbers under consideration.
| Population | Sample |
|---|---|
| It is the complete set of all observations pertaining to a single characteristic of interest. | It is the set of values that are actually collected in the course of an investigation. |
Example 2.
In the last example, in our school there are more than eigth persons, but we haven´t enough time to ask all of them for the program of tv they saw last night, for this reason, we only ask to eight friends.
In this example, the population are all pupils of our school, and the sample are our eigth friends.

Quantitative data discrete and continous.
| Quantitative data discrete | Quantitative data continuous |
|---|---|
| The values are in integers (whole numbers), for example the number of person that are seen the television, the numbers of the lotery, etc. | The values are in numerical measurements, for example the weight, the temperature, the size, etc. |
Quantitative data continuous
In this case we group together observations that have valous close to each other so that instead of having a large number of values, each with a small number of observations, we have a smaller set of intervals, each containing a larger number of observations. We group these data by dividing the interval of numbers that contains all the values of the data into smaller intervals, called classes. The interval of values in each case is called a class. The class limits are the highest and lowest values specified for each class. The center of an interval, called class mark, is equal to half the sum of the class limits.
Frequency and relative frequency
Frequency (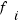 ) ) | Relative frequency (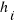 ) ) |
|---|---|
The frequency (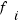 ) of a value is the number of times the value occurred in our study. ) of a value is the number of times the value occurred in our study. | The relative frequency (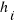 ) of a value is equal to the number of observations(frequency) divided by the total number of observations N (total frequency), ie, ) of a value is equal to the number of observations(frequency) divided by the total number of observations N (total frequency), ie, 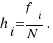 |
Example 3: height in the classroom.
The average.
The average of a set of n values 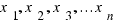 is the sum of these values divided by the number of values, n.
is the sum of these values divided by the number of values, n.
- For qualitative data discrete:
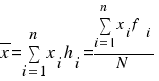 , where
, where 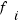 is the frequency,
is the frequency, 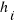 is the relative frequency and N is the total number os observations. (
is the relative frequency and N is the total number os observations. (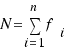 ).
).
Example 4: the cards in the soccer.
 We will do a study of the yellow and red cards that the referees have showed in 15 matchs of a league of soccer. We know the following results:
We will do a study of the yellow and red cards that the referees have showed in 15 matchs of a league of soccer. We know the following results:
NOTE: 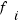 is the number of matchs of whom the referee showed x yellow (or red) cards in each match.
is the number of matchs of whom the referee showed x yellow (or red) cards in each match.
1.-What is the average of yellow cards in each match in the league of soccer?
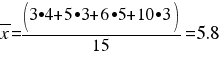
ie, the referee have showed 5.8 yellow cards in each match in the league, of average.
2.-What is the average of red cards in each match in the league of soccer?
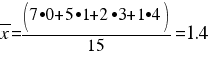
ie, the referee have showed 1.4 red cards in each match in the league, of average.
- For qualitative data continous we take the variable value as the class mark.