THE COMPLEX NUMBERS.
We said that an equation with ∆ < 0 has not solution, beacuse we didn´t know to do the square root of a negative number.
In a moment of the history, the mathematics invented a number to these equation had solution. This number was called imaginary unit: 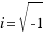
If the imaginary unit is combined with two real numbers a, b by the processes of addition and multiplication, we obtein a complex number a+bi. a and b are the real and imaginary part of the complex number. If a=0, the number is said to be purely imaginary; if b=0, it is of course real. Zero es the only number which is at once real and purely imaginary. Two complex numbers are equal if and only if they have the same real part and the same imaginay part.
The transformation which replaces a+bi by a-bi is called complex conjugation, and a-bi is the conjugate of a+bi.
The geometric representation of complex number.
The complex number z=a+bi can be represented by the point with coordinates (a,b). The first coordinate axis (x-axis) takes the name of real axis, and the second coordinate axis (y-axis) is called the imaginary axis. The plane itself is referred to as the complex plane.
Ejemplo:

Arithmetic operations
Addition: 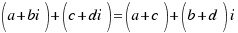
Substract: 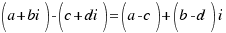
Multiplication: 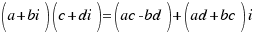
NOTe: If we multiply a complex number by its conjugate, the results is always a real number:
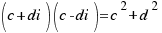
Division: 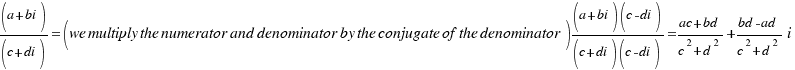
NOTe: We can´t divide by zero.
Polar coordinates.
If z=a+bi is a complex number, maybe we need to express this complex number with polar coordinates.
The polar coordinates of the point (a,b) are (r,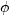 ). We know that:
). We know that:
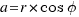
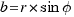 .
Now, we can write:
.
Now, we can write: 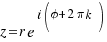 , con k = 1,2, ……
, con k = 1,2, ……
or 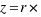 . In this trigonometric form of a complex number r is always > or equal zero and is called the modulus. The polar angle
. In this trigonometric form of a complex number r is always > or equal zero and is called the modulus. The polar angle 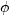 is called the argument of the complex number, and we denote it by arg(z).
is called the argument of the complex number, and we denote it by arg(z).
