ECUACIONES DE SEGUNDO GRADO BÁSICAS
Ejemplo
Primero vamos a ver una demostración visual de una ecuación de segundo grado con un ejemplo:
Resolvamos la ecuación 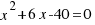 .
.
Solución
Pasamos el término independiente al otro miembro: 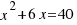 .
.
El primer sumando 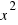 , se corresponde con el área del cuadrado de lado
, se corresponde con el área del cuadrado de lado 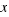 , y el segundo sumando
, y el segundo sumando 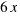 , se corresponde con el área del rectángulo de lados
, se corresponde con el área del rectángulo de lados 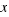 y
y 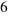 , como se indica en el siguiente dibujo:
, como se indica en el siguiente dibujo:

El rectángulo lo descomponemos en dos rectángulos iguales de lados 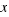 y
y 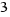 , y pasamos uno de ellos justo debajo del cuadrado de lado
, y pasamos uno de ellos justo debajo del cuadrado de lado 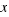 .
.

Y ahora, se añade el cuadrado de área 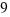 del espacio que queda en la esquina inferior derecha de la figura, y así obtenemos un cuadrado perfecto de lado
del espacio que queda en la esquina inferior derecha de la figura, y así obtenemos un cuadrado perfecto de lado 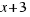 .
.
Como hemos añadido un cuadrado de área 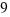 , hemos modificado nuestra ecuación inicial, y por tanto, ahora tenemos que sumar
, hemos modificado nuestra ecuación inicial, y por tanto, ahora tenemos que sumar 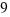 a ambos miembros de la ecuación, obteniendo:
a ambos miembros de la ecuación, obteniendo: 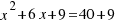 , así el miembro de la izquierda de la ecuación es el cuadrado perfecto:
, así el miembro de la izquierda de la ecuación es el cuadrado perfecto: 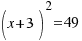 .
.
Haciendo la raíz cuadrada en los dos miembros nos queda:
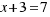
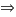
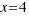
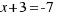
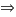
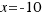
La solución 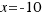 no tiene sentido en geometría (por ser un resultado negativo), pero sí es solución de la ecuación dada.
no tiene sentido en geometría (por ser un resultado negativo), pero sí es solución de la ecuación dada.
Ejercicio.
Intenta resolver la ecuación 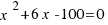 , de la misma manera que lo hemos hecho en el ejemplo anterior. Como ayuda te damos la siguiente aplicación con la que puedes practicar las figuras que van quedando al resolver la ecuación. Para ello, toma el punto
, de la misma manera que lo hemos hecho en el ejemplo anterior. Como ayuda te damos la siguiente aplicación con la que puedes practicar las figuras que van quedando al resolver la ecuación. Para ello, toma el punto  del segmento que hay arriba a la izquierda de la aplicación y muévelo según creas conveniente.
del segmento que hay arriba a la izquierda de la aplicación y muévelo según creas conveniente.
Si no se puede ver la siguiente aplicación, se puede descargar JAVA en la dirección: http://www.houspain.com/gttp/salsaj
Caso general
Ahora hacemos los mismos pasos para una ecuación de segundo grado en general: 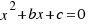 , y llegaríamos a la solución
, y llegaríamos a la solución 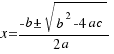 . El radicando
. El radicando 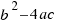 recibe el nombre de discriminante.
recibe el nombre de discriminante.

Tenemos la ecuación 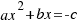 , multiplicamos los dos miembros de la ecuación por
, multiplicamos los dos miembros de la ecuación por 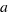 para que nos quede un cuadrado perfecto de lado
para que nos quede un cuadrado perfecto de lado 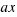 , y así nos será más sencillo operar, entonces nos queda la ecuación
, y así nos será más sencillo operar, entonces nos queda la ecuación 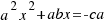 .
.
El primer sumando 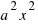 , es el área del cuadrado de lado
, es el área del cuadrado de lado 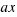 y el segundo sumando
y el segundo sumando 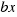 , es el área de un rectángulo de lados
, es el área de un rectángulo de lados 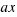 y
y 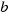 .
.
Descomponemos el rectángulo en otros dos rectángulos de lados 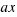 y
y 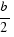 , como se observa en la figura siguiente:
, como se observa en la figura siguiente:

Añadiendo el cuadrado de área 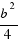 que falta en la figura (esquina inferior derecha), tendremos un cuadrado perfecto de lado
que falta en la figura (esquina inferior derecha), tendremos un cuadrado perfecto de lado 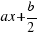 , entonces sumamos
, entonces sumamos 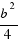 a los dos miembros de la ecuación, quedándonos:
a los dos miembros de la ecuación, quedándonos: 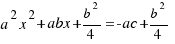 , multiplicamos los dos miembros por 4 para que nos quede más sencillo:
, multiplicamos los dos miembros por 4 para que nos quede más sencillo: 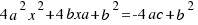 .
.
El miembro de la izquierda de esta última ecuación es el siguiente cuadrado perfecto: 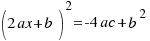 .
.
Haciendo la raíz cuadrada en los dos miembros queda:
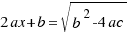
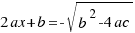
Por tanto, las soluciones a nuestra ecuación 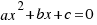 son (despejando
son (despejando 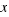 de las dos últimas ecuaciones):
de las dos últimas ecuaciones):
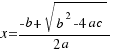
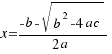
Al radicando 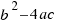 lo llamaremos discriminante y lo representaremos con la letra
lo llamaremos discriminante y lo representaremos con la letra 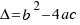 . Podemos tener varios casos en las soluciones de nuestra ecuación según sea el discriminante:
. Podemos tener varios casos en las soluciones de nuestra ecuación según sea el discriminante:
1.- Si ∆ > 0, la ecuación 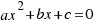 tiene dos soluciones reales y distintas:
tiene dos soluciones reales y distintas:
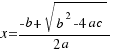
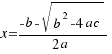
2.- Si ∆ = 0, la ecuación 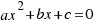 tiene una solución doble:
tiene una solución doble:
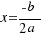
3.- Si ∆ < 0, la ecuación 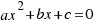 no tiene soluciones reales.
no tiene soluciones reales.




