- Descarga la siguiente fotografía de Luna pinchando sobre ella
- Abre la fotografía que has descargado con el programa SalsaJ
- Pon la escala correspondiente a la fotografía en SalsaJ conociendo como dato el diámetro de la Luna (3.476 Km)
- Los círculos azules de la fotografía indican posibles montañas de la Luna a estudiar
- Determina la distancia que hay entre el terminador y la cumbre de la montaña (el segmento
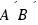). Con la palabra terminador se conoce la división existente entre los hemisferios iluminado y no iluminado de la Luna o de cualquier otro cuerpo celeste - El dato del radio lunar es conocido ya que tenemos el valor del diámetro de la Luna
- Identifica -en la figura del apartado 10- un triángulo rectángulo
- Aplica el teorema de Pitágoras en el triángulo rectángulo identificado en el apartado anterior
- Cambia los segmentos por sus equivalentes medibles: d, a y R. (observar figura del siguiente apartado)
- Calcular la altura de la montaña, utilizando la teoría de ecuaciones de segundo grado, teniendo en cuenta la siguiente figura:
A´= cumbre de la montaña
A´B´= d = distancia de la cumbre de la montaña al terminador
AA´= a = altura de la montaña
OA = R (radio de la Luna)
NOTA: la solución dará en función de R y d.
