0. Descarga una de las siguientes fotografías pinchando en ella


Monte Pico Monte Piton
- Con el programa Salsa J, abre la fotografía que has descargado (recuerda que lo puedes instalar a través de http://www.houspain.com/gttp/salsaj)
- Los círculos azules señalados en cada fotografía indican dos montañas a estudiar: el monte Pico y el monte Pitón
- Necesitarás el diámetro de la Luna -3.476Km- para que el programa SalsaJ calcule la relación de escala entre los Km en la Luna y los píxeles de la fotografía
- Calcula la distancia que hay entre el terminador y la sobra de la montaña (el segmento TB). Llamaremos terminador a la línea imaginaria que separa el lado iluminado y del no iluminado de la Luna o de cualquier otro cuerpo celeste
- El radio de la Luna es un dato conocido, ya que sabemos el valor del diámetro de la Luna
- Determinamos la longitud de la sombra de la montaña de la Luna (segmento AM)
- Calculamos la altura de la montaña, teniendo en cuenta la siguiente figura y los siguientes puntos:
- El segmento 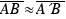 debido a que la curvatura es despreciable, ya que la altura de la montaña es mucho menor que el radio de la Luna
debido a que la curvatura es despreciable, ya que la altura de la montaña es mucho menor que el radio de la Luna
- Cuanto más cerca del terminador esté la montaña menor será el error debido a la curvatura 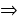 TB se considera recta
TB se considera recta
- ¿Cómo llegamos a la siguiente figura en el plano?

BM = altura de la montaña (nuestra incógnita)
OB = radio de la luna (conocido por el problema del diámetro de la luna)
AM = longitud de la sombra de la montaña (la hemos calculado con Salsa J)
TB = distancia de la montaña al terminador (la hemos calculado con Salsa J)
- El ejercicio no ha terminado hasta que estimes si tu resultado es aproximado a la altura real. Para ello, busca la altura de los dos montes por internet.
- En caso de que tu resultado se diferencie del real en más de un 20%, revisa cada uno de los pasos y cálculos que has realizados.




