ESTADÍSTICA
¿QUÉ ES LA ESTADÍSTICA?
- La estadística: se encarga de la interpretación y el análisis de datos. Para ello, tenemos que recopilar una serie de datos que representaremos en una gráfica (diagramas de barras, polígonos de frecuencias,…) y de los que haremos un análisis. Lo que buscamos son condiciones regulares en fenómenos aleatorios.
Ejemplo 1: ¿qué vemos en la tele?
 Podemos preguntar a 8 amigos del colegio qué programa de televisión vieron anoche. Con estos datos podemos hacer un estudio y sacar varias conclusiones:
Podemos preguntar a 8 amigos del colegio qué programa de televisión vieron anoche. Con estos datos podemos hacer un estudio y sacar varias conclusiones:

Así, obtenemos el siguiente diagrama de círculo con los porcentajes de los amigos que ayer vieron en la tele las diferentes opciones:

POBLACIÓN Y MUESTRA
| Población | Muestra |
|---|---|
| Es la cantidad total de elementos que forma parte de un estudio estadístico determinado. | Es un subconjunto de la población. |
Ejemplo 2: continuamos viendo la tele
Siguiendo con el ejemplo anterior, imaginemos que en nuestro colegio hay más de ocho personas, y no nos da tiempo a preguntarles a todas qué programa de televisión vieron anoche. Hacemos la encuesta a ocho personas del colegio elegidas por nosotros.
En este ejemplo, la población serían todos los alumnos del colegio. La muestra los ocho alumnos que escogemos para realizar nuestro estudio.
VARIABLE ESTADÍSTICA DISCRETA Y CONTINUA
| Variable estadística discreta | Variable estadística continua |
|---|---|
| Toma valores puntuales, como por ejemplo el número de personas que están viendo un programa, números premiados en la lotería, etc. | Puede tomar cualquier valor de un intervalo de numeración, como por ejemplo la talla, el peso, la temperatura, etc. |
VARIABLE ESTADÍSTICA CONTINUA
Cuando la variable estadística es continua, es más conveniente agrupar los valores en intervalos que tratarlos individualmente. Para ello hacemos una división en tantas partes iguales como intervalos queramos considerar. Los intervalos en que se agrupan los datos reciben el nombre de clases. La diferencia entre los extremos de la clase se llama amplitud de la clase y ésta debe ser igual para todas. El valor medio de cada clase se llama marca de clase y se representa por 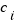 . Para calcular este valor se suman los extremos y se divide por dos. Los extremos de cada clase se llaman límite inferior y límite superior de la clase.
. Para calcular este valor se suman los extremos y se divide por dos. Los extremos de cada clase se llaman límite inferior y límite superior de la clase.
FRECUENCIAS ABSOLUTAS Y RELATIVAS
Frecuencia absoluta (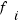 ) ) | Frecuencia relativa (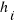 ) ) |
|---|---|
La frecuencia absoluta (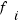 ) de un valor de la variable es el número de veces que se repite ese valor. ) de un valor de la variable es el número de veces que se repite ese valor. | La frecuencia relativa (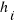 ) de un valor de la variable es el cociente entre la frecuencia absoluta de ese valor y el número total de datos N, es decir, ) de un valor de la variable es el cociente entre la frecuencia absoluta de ese valor y el número total de datos N, es decir, 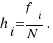 |
Ejemplo 3: estaturas de la clase.

Tenemos las estaturas de 40 alumnos de un colegio de Toledo que colocamos en una tabla de la siguiente forma:

LA MEDIA ARITMÉTICA
Llamamos media aritmética de una variable al cociente entre la suma de todos los valores de la variable y el número de valores. La media no es, en general, un valor de la variable.
- Si la variable es discreta:
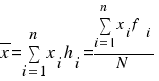 , donde
, donde 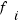 es la frecuencia absoluta,
es la frecuencia absoluta, 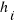 es la frecuencia relativa y N es el número total de datos (
es la frecuencia relativa y N es el número total de datos (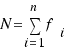 ).
).
Ejemplo 4: los árbitros y sus tarjetas en el fútbol.
 La liga de fútbol colegial quiere realizar un estudio sobre el “juego limpio”. Para ello estudia el número de tarjetas rojas y amarillas que se han sacado en los 15 partidos de competición. Los resultados obtenidos son los siguientes:
La liga de fútbol colegial quiere realizar un estudio sobre el “juego limpio”. Para ello estudia el número de tarjetas rojas y amarillas que se han sacado en los 15 partidos de competición. Los resultados obtenidos son los siguientes:


NOTA EXPLICATIVA: 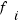 nos indica el número de partidos en los cuales el árbitro ha sacado x tarjetas amarillas (rojas, respectivamente) en cada uno de los partidos.
nos indica el número de partidos en los cuales el árbitro ha sacado x tarjetas amarillas (rojas, respectivamente) en cada uno de los partidos.
1.-¿Cuál es el número medio de tarjetas amarillas por partido a lo largo de la liga?
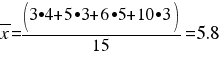
Es decir, 5.8 tarjetas amarillas ha sacado el árbitro de media por partido jugado a lo largo de la liga.
2.-¿Y el número medio de tarjetas rojas?
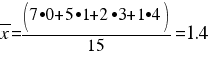
Es decir, 1.4 tarjetas rojas ha sacado el árbitro de media por partido jugado en la liga de fútbol colegial.
- Cuando la variable es continua se toman como valores de la variable las marcas de clase.
Ejemplo 5: los recién nacidos.
Tenemos los datos sobre el peso de 100 recién nacidos recogidos en la tabla siguiente:

En este caso la media queda:
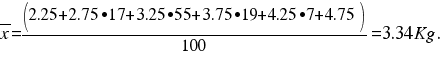
Ejercicios relacionados
En cada ejercicio se indica qué otros conocimientos son necesarios.





