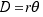
Veamos cómo llegamos a este resultado:
Tenemos la siguiente situación:

Partimos del triángulo rectángulo coloreado

Por ser un triángulo rectángulo, se aplican las razones trigonométricas sobre el ángulo 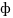
y obtenemos que 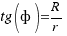 .
.
Además, como 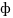 es un valor muy pequeño, podemos tomar la aproximación
es un valor muy pequeño, podemos tomar la aproximación 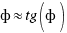
Así que, de la expresión anterior se tiene que 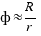 y como
y como 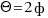 , entonces
se tiene que
, entonces
se tiene que 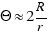 .
.
Lo que estamos buscando es el diámetro de la Luna, al que hemos llamado D en la figura.
Sabemos que el diámetro es dos veces el radio, por lo que 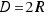 .
.
Sustituyendo nos queda: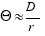 .
.
Y despejando D, que es lo que buscamos, tenemos 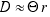 .
.




