Radians and 0.0174
Definition
Angles can be measured in different units; degrees or radians.
A radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.
First idea
If some dynamic worksheets are not available, java can be download from thepage:
What a radian is?
Let's show the definition above on the next dynamic worksheet:
- Move the yellow point and the radius in order to make the arc and the radius equals in length.
- How long is the angle
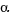 measured in degrees?
measured in degrees? - Observe the resoult when we divide arc length by radius. It is 1. So, that angle is one radian, expressed in degrees.
- Could you do it with another radius? Do you get the same angle?
- Make
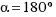 , how many radians do you think it is?
, how many radians do you think it is?
Observe the result of the division on the worksheet. Is this number familiar? - Try it with
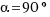 ,
, 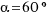 ,
, 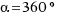 . Do you know how many radian are?
. Do you know how many radian are? - Do you come to a conclusion about a relationship between degrees and radians?
Formally
How many degrees is 1 radian?
Let's work out what we have conclude above, the relationship between degrees and radians.
We know what the definition says:
A radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle.
So we have to make equal the arc length and the length of the radius.
An arc of circumference (circle) is the porcion of the circumference between two radius.
Arc Length 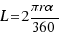 ,
,
with r = radius
and 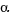 angle of the arc in degrees.
angle of the arc in degrees.
Following the definition, we have to make equal the radius r and the arc length, this is:
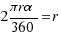 .
.
Then, we have 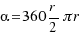 ,
,
smplifying 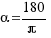 wich is 1 radian in degrees.
wich is 1 radian in degrees.
Relationship between degrees and radians
There are 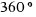 in a circumference, this is
in a circumference, this is 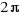 radianes.
radianes.
So, 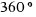 are
are 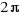 radianes.
radianes.
This is very useful because we can make cross-multiplication with this and then we can obtein radians from degrees and degrees from radians:
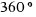 ———
——— 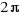 radians
radians
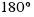 ———- x radians
———- x radians
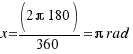 (so
(so 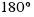 are
are 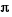 radians)
radians)
Using cross-multiplication again:
- Find out how many degrees is 1 radian.
- Find out how many radians is 1 degree.
In practice
From degrees to radians and from radians to degrees
You can use similar Thales' theory to do the next exercises:
- How many radians are
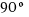 ,
, 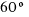 ,
, 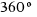 and
and 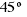 ?
? - How many degrees are
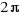 rad,
rad, 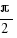 rad,
rad, 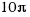 rad and
rad and 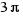 rad?
rad?
Check your answers here.




